5变化电磁场产生引力场的试验及简化版的理论推导

作者张祥前交流微信18714815159

变化电磁场产生引力场试验已经申请了专利——“一种电磁转化引力场装置”。

专利.png

人工场就是变化电磁场产生的可以人工控制的引力场。人工场可以取代我们地球上流行的电能，使人类进入光速虚拟时代。

要想人工场在地球上变成现实，最关键的是变化电磁场产生引力场的试验取得成功。

2023年11月2日，本人试验中首次发现：加速运动正电荷产生加速度方向相反的引力场。

2024年3月1日又发现：变化磁场产生漩涡引力场，令一切物体旋转。

1，加速运动正电荷产生加速度方向相反的直线引力场试验。

在下图中，

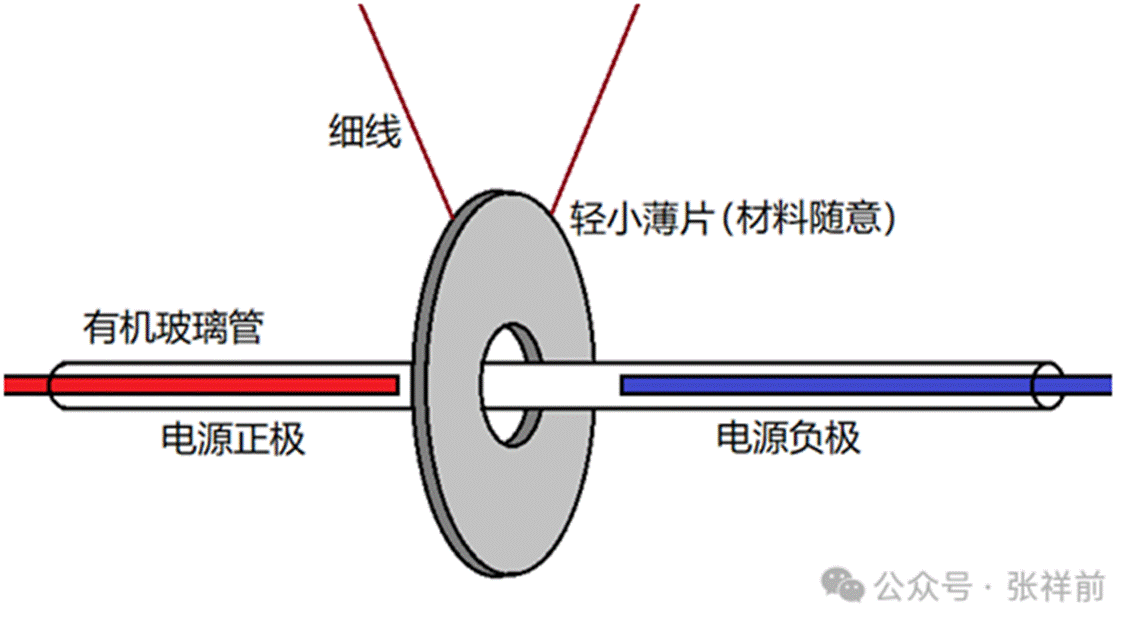
导线的正负极之间不接触，相隔6厘米，套上有机玻璃管。

用细线悬挂一个轻小薄片状物体【任意一种材料】，中心打孔，套在有机玻璃管上，但不接触有机玻璃管，处于正负极6厘米空隙的中间位置上。

当正负极连接5万伏以上的高压直流电源，按下电源开关瞬间，悬挂物向正极方向运动。掉转正负极，悬挂物仍然向正极方向运动。

按照统一场论的变化电磁场产生引力场理论来分析，当按下开关瞬间，线路中正电荷原地加速振动，在正负极之间产生的加速电动势就包含了引力场A，数学公式为：

Eθ/er = A×R/c²

上式中Eθ是正点电荷加速运动产生的扭曲正电场【矢量形式】，er是电荷静止时候产生的静电场【标量形式】，R是由电荷指向空间中的一个考察点的位置矢量，c是标量光速。

详细的数学推导，参阅《统一场论》，加张祥前微信18714815159可以获得电子版资料。

这个由加速电场产生的引力场令各种材料的悬挂物加速运动。

套上有机玻璃管，是防止离子风效应和静电马达效应。让悬挂物是薄片状，为了抑制悬挂物的极化效应和退极化效应。

在真空条件下这个试验也取得了成功。

以上试验，由于有机玻璃管不方便弯曲，有机玻璃管两端的导线接头部分容易产生离子风，后来，用柔软的硅胶管代替有机玻璃，取得很理想的效果。

在下图中：

用一根长190厘米，外径3mm【或者2mm】，内径1mm的硅胶管，把两根长90厘米、直径0.8mm漆包铜导线套上。两个导线不接触，相隔5厘米。

如果导线不好塞进硅胶管，可以对硅胶管内滴润滑油，或者用医用注射针注油进去。

导线和硅胶管悬吊在一个木制的架子下面。

制作一个4cm×11cm、厚度0.15mm的塑料皮，用细棉线悬挂起来，位置在两根导线空隙的中心点。塑料皮中心打孔，套在硅胶管上，但不接触硅胶管。

两根导线分别接在两个串联的高压包的正负极上。给两个高压包供电的，可以是电池、电源机箱【输入220v交流电，输出直流0至30v，淘宝上可以买到】。如果给两个高压包独立供电，效果要好一些。

从淘宝首页上搜“直流2000Kv高压发生器高压模块”，可以买到高压包。选择输入直流电压7.4v的。

高压包输出2000Kv是商家虚标，实际测量在20kv左右。

怎么鉴别高压包高压输出端两根线的正负极？

把高压输出端两根线离开8至10厘米，下面点上蜡烛，让高压包通电，火焰偏向那一方，就是负极。或者用高压直流电表测量。

我在试验时候，按下电源，塑料皮向正极移动，调转正负极，塑料皮仍然向正极运动。

按照《统一场论》理论的预言：当按下开关瞬间，加速运动正电荷产生加速度方向相反的引力场。

线路中正电荷原地加速振动，在正负极之间产生的电动势就包含了引力场，这个引力场令悬挂物加速运动。

导线套上硅胶管，是防止离子风效应和静电马达效应。让悬挂物是薄片状，是为了抑制悬挂物的极化效应和退极化效应。

试验的关键是把导线【特别是导线接头】绝缘、密封彻底，把高压包覆盖起来，不能让导线和高压包对外产生离子风和静电马达效应。

试验的时候要注意，不能在短时间里反复试验，那样极化效应和退极化效应严重，可能使塑料皮运动方向紊乱。

高压包不是必须的，高压包输出的脉冲直流电杂波严重，对试验有干扰，几个串联和并联就更严重，高压包只是价格便宜而已。其他4万伏以上的直流高压效果要更好一些。

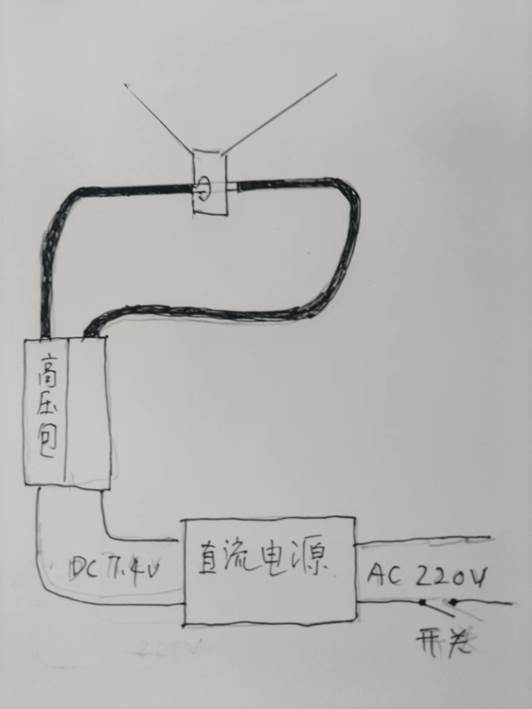
以上是两个高压包串联试验的电路图。

2，磁场变化产生漩涡引力场令一切物体旋转试验

在下图中：

横放的真空罐直径10厘米，里面悬挂一个红色的聚乙烯小球，小球质量0.35克，试验的时候抽成真空。抽真空的目的是防止静电马达效应和离子风效应。

真空罐上下各放置一个直径8厘米、高12厘米硅胶导线绕的线圈，这个红色硅胶导线直径10毫米，里面的铜丝直径1.5毫米。

两个线圈相互不连接，是断开的，两个线圈导线的断点处不做绝缘处理，外面套一个8厘米长的硅胶管子，管子的另一个端点不封闭，是开放的。

在下面的示意图中，标出了两个端点的位置是在同一个平面上，但是，是错开的。想象一下，是两个螺旋管，虽然断开了，但是，在空间中暗暗地以螺旋式走向连接上了。

两个线圈的另一个端点分别接脉冲直流高压电的正负极。

我最近的试验使用了两种电源，一种是下图的：

2GF-200KV/5mA直流高压发生器，图中的红色柱子是倍压筒。

一个线圈接这个高压发生器的高压输出端，一个线圈接地线。

试验的时候，真空罐抽成真空，当电压调到2万伏，电流调到2万分之一安培的时候，真空罐里面的聚乙烯小球开始旋转。

这个试验采取高压、超低电流供电，使线圈产生的极化效应大幅度下降，突出了变化磁场产生漩涡引力场效应。这个试验比较稳定，几乎每一次试验都能够成功。

其他试验，在电流大的情况下，极化效应很强，像是把聚乙烯小球按住，小球不旋转，使试验有时候失败。

以下是大功率倍压电路提供的高压脉冲直流电。

图中地下白色的是2000瓦直流电源。

这个直流电源把50赫兹、220伏家用交流电变成直流电，试验的时候调到52伏。

52伏直流电经过3000瓦zvs驱动板振荡为频率3万赫兹、18伏交流电，交流电经过图中黑色的550倍变压器，变成1万伏直流电。

1万伏交流电经过10倍压电路【16倍压效果更好，图中绿色的是2CL - 100KV - 2A整流二极管，黄色的是30kv高压电容】整压和升压，变成了10万伏的脉冲直流电。

试验的时候，按下电源开关，真空罐里面的小球开始旋转，关电源的时候，小球旋转加快。

这个试验偶尔失败，原因是zvs驱动板有时候电压没有升起来，有时候极化效应太强，还有其他复杂的原因，有待分析。

以下是断电后令聚乙烯小球旋转试验。

用直径0.57毫米的漆包铜线绕两个长19厘米，直径3.7厘米的螺旋线圈。线圈中间是厚度1毫米的纸筒子。

上面的线圈一端接两个串联的高压包【高压包输入是直流7.4伏，输出高压脉冲，淘宝上商家标200万伏，那是虚标】的负极，一端放在真空罐【直径10厘米】上。

下面的线圈上端贴上真空罐，下端连接高压包的正极。两个线圈相隔10厘米，彼此没有连接。

中间横放的真空罐，已经抽成真空，里面用细棉线悬挂一个红色的聚乙烯小球。细棉线一端是用AB胶固定在真空罐内壁上。

当按下电源开关，聚乙烯小球旋转了起来。试验发现以磁力线为轴线旋转。

以上试验在真空条件下，可以排除静电马达效应、离子风效应。因为离子风是空气被电离形成的，真空里没有空气，所以不存在离子风效应。

静电马达效应，是正负极导线喷射电荷或者离子到聚乙烯小球上形成的。

而电极在真空罐外，隔着真空罐厚玻璃，无法将电荷喷射到真空罐里面去。

但不能排除电场的极化效应，因为高电压的极化效应不但在真空中存在，而且可以轻易的穿过真空罐的厚玻璃。

这种线圈上下结构，线圈和悬挂聚乙烯小球的细线平行，使得极化效应产生的力沿细线平行方向，而聚乙烯小球以细线为轴线旋转，这样，极化效应对旋转就没有了贡献。

这种情况下，可以基本上排除极化效应对旋转快慢的影响，加上排除了静电马达效应和离子风效应，只剩下了统一场论的变化磁场产生漩涡引力场令一切物体旋转的效应。

需要注意的是，极化效应和变化电场产生直线式引力场效应在一定程度上干扰了悬挂物的旋转方向。

所以，试验的时候，不能连续反复的试验，反复的试验使材料被极化严重。

使用细漆包线绕线圈，线圈绕的匝数很多，可以突出磁场的旋转效应，降低电场的直线式运动效应。

用细漆包线绕线圈，线圈绕的匝数很多，线圈总质量比较大，可以增加线圈的电感能量。当电源关掉后，线圈储存的能量，仍然可以令悬挂物旋转。

这种情况下，极化效应、变化电场令物体直线运动效应消失，只剩下了变化磁场产生漩涡引力场令物体旋转效应。这样便于我们分析。

在下图中：

直径7厘米、高18厘米的一个不锈钢法拉第笼，里面用细棉线悬挂一个高5厘米，直径2.7厘米的红色聚乙烯小球。

法拉第笼子左右两边各放置一个直径3.7厘米，长19厘米【用直径0.57毫米的漆包线绕在厚度1毫米的纸筒子上】，线圈接2个串联的高压包【标注7.4V2000kv】的正负极上。用直流电源机箱给高压包供电。

不锈钢法拉第笼下面用AB胶粘结一个直径0.6厘米、高21厘米的塑料管子，塑料管下面插在一个套管里，目的是为了让法拉第笼子笔直的落下，不乱摆。

塑料管里面用AB胶粘结一根棉线，棉线的另一端拴在下面的漏保开关上。

不锈钢法拉第笼上面的盖子被固定住，当拉下漏保开关，切断电源，稍后，漏保开关连着的棉线，会把法拉第笼子打开，法拉第笼子的下部分会坠落下来。

我在试验的时候，打开电源，处于法拉第笼子里的聚乙烯小球不动。

按照统一场论理论，电路在开和关的时候，里面的正电荷原地加速振动，产生了扭曲正电场，这个扭曲正电场包含了漩涡磁场和漩涡引力场。

这种引力场和地球的直线散度引力场不一样，在场源附近不能穿透法拉第笼子，这个道理如同法拉第电磁感应的磁变电，如果屏蔽了磁，也就没有了电。

这里的引力场是加速电场产生的，法拉第笼子屏蔽电场，也就没有了引力场。

当我按下下面的漏保开关，电源切断，稍后，漏保开关连着的棉线把法拉第笼子打开。让里面的红色聚乙烯小球暴露出来。

结果发现，红色小球在断电后居然持续的旋转起来。

这个试验很重要，因为是在断电状态下下，聚乙烯小球仍然在旋转，这个试验可以排除极化效应、静电马达效应、离子风效应。

这三个效应都是通电状态下才有。

而且，聚乙烯小球在线路刚通电的情况下，呆在法拉第笼子，是不会受到到极化效应、磁场效应影响的。

这个试验表示断电的情况下，仍然有漩涡效应，这个不用统一场论的变化电磁场产生引力场，不用场效应，无法解释。

可能大家一个疑问：

断电那一瞬间，变化的电磁场没了，由它而生引力场不也就没了吗，为啥聚乙烯还会动呢？

按照统一场论，电路开和关的时候，会引起正电荷原地加速振动，产生一个扭曲正电场，这个扭曲正电场包含了漩涡磁场和和漩涡引力场，并且，这个扭曲正电场以光速向四周传播开。

从能量的角度看，是线圈的电感能量。

从场效应看，是光速传播的扭曲正电场对空间的扭曲效应。

线圈通电的时候，让线圈储存了电感能量，当附近有悬挂的聚乙烯小球，磁场储存的能量以漩涡引力场令小球旋转运动释放出来。

我在后来的试验中，把高压包输出的正负极分别接上一个中心有硅钢片的大线圈，增加了线路的电感能量，结果使聚乙烯小球旋转的时间更长。

如果附近没有悬挂聚乙烯小球，而是连接了一个灯泡，磁场储存的能量会以电场令灯泡发亮的形式，把磁场储存的能量释放出来。

这个实验关掉了总电源，没有了离子风效应、静电马达效应、极化效应和退极化效应的干扰，便于我们展开分析，使分析问题简单起来。

这个试验也要注意，不能在短时间里连续反复的试验。

【附录】变化电磁场产生引力场试验的理论推导。

以下是变化电磁场产生引力场的理论推导过程。详细的推导过程见《统一场论》，加本人微信可以获得《统一场论》电子版资料。

以下变化电磁场产生引力场试验的理论推导。

1，基本假设

宇宙任何物体，周围空间总是以矢量光速C’【本文大写字母为矢量】、以圆柱状螺旋式向四周发散运动。

在统一场论中，圆柱状螺旋式运动的直线运动部分是电场，旋转运动部分是磁场，旋转指向中心轴线的加速度是引力场，三场相互垂直。

静止物体周围也有磁场，只是在一个曲面上有多少磁场线穿进去，就有多少磁场线穿出来，相互抵消了，对外不显效应。

以上基本假设提到了空间本身在运动。

为了描述空间本身的运动，我们把空间分割成许多个小块，每一个小块叫空间点，通过描述空间点的运动，就可以描述空间本身的运动。

以上基本假设提到了矢量光速。

本文认为光速可以扩展到矢量，矢量光速的方向可以变化，模是标量光速，用小写字母c表示，c不变。

当物体粒子o点相对于我们观察者静止，周围一个空间点p以矢量光速C’向四周发散运动，当o点以速度V相对于我们运动，p点相对于我们观察者的速度我们用矢量光速C表示。

C’和C大小相等，方向不同。C’和C的关系是否符合相对论的洛伦茨变换？

按照洛伦茨的速度变换，C’的三个分量Cx’，Cy’， Cz’和C的三个分量Cx，Cy，Cz满足的关系为：

Cx’ = (Cx – v)/[1- (Cx v/c²)]

Cy’ = [Cy√（1-v²/c²）]/ [1- (Cx v/c²)]

Cz’ = [Cz√（1-v²/c²）]/ [1- (Cx v/c²)]

由以上可以导出：

（Cx’）²+（Cy’）²+（Cy’）²

= [(Cx– v)²+ Cy²（1-v²/c²） + Cz²（1-v²/c²） ]/[1- (Cx v/c²)]²

= c²c²[Cx²+ Cy²+ Cz²-2 Cx v+ v²-（c²-Cx²）v²/c²]/（c²-Cx v)²

= c²c²[c²-2 Cx v+ v²-（c²-Cx²）v²/c²]/（c²-Cx v)²

= c²[c²c²-2 c²Cx v+ Cx²v²]/（c²-Cx v)²

= c²

由此导出矢量光速C和C’满足以下关系：

C’·C’ = C·C = c²

C和C’方向不一样，但是，数量是一样的。

当o点相对于我们观察者以速度V运动的时候，设空间点p点相对于o点的速度为U，由于C是U和V的合成，也就是C=U+V，

所以：

U=C-V

2，认识引力场

我们站在地球上，随手放下一块石头，石头以加速度自由落体向地球中心坠落。

如果没有石头，石头所在的空间仍然以那种方式在向地球中心坠落，这个就是引力场的本质。

引力场的本质就是物体周围空间本身向物体质心加速运动的加速度。

引力场有两个重要的性质：

由物体指向引力场中的一点【我们叫场点，或者叫考察点】的位置矢量，与引力场方向相反。

引力场可以对一切材料构成的物体有加速作用。

3，认识磁场

人类发现，带电粒子相对于我们观察者以匀速直线运动引起运动速度垂直方向的电场变化，电场变化部分可以认为就是磁场，也就是随速度变化的电场产生磁场。

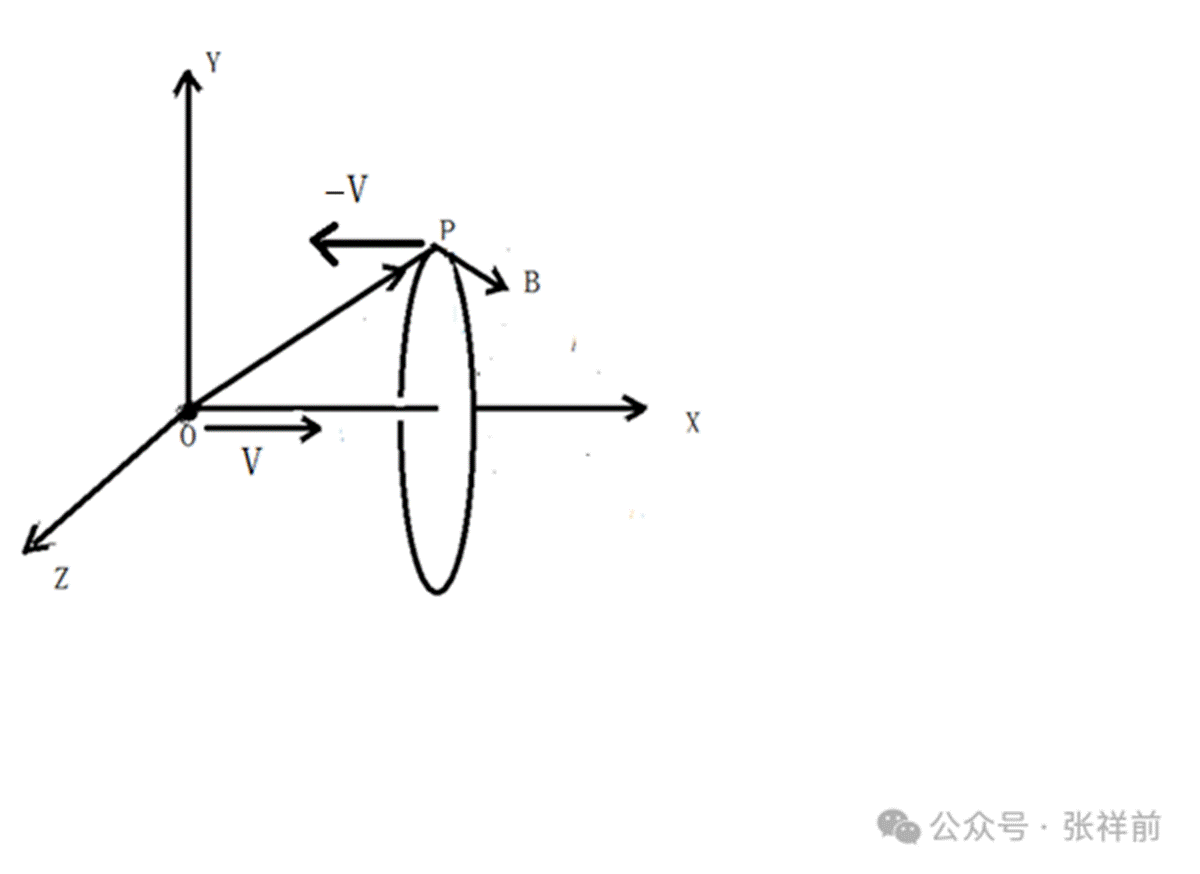
在下图中，一个相对于我们静止的正电荷粒子o点，在周围空间点p处产生了静电场E’。当o点相对于我们观察者以速度V沿x轴正方向匀速直线运动，可以产生磁场B。

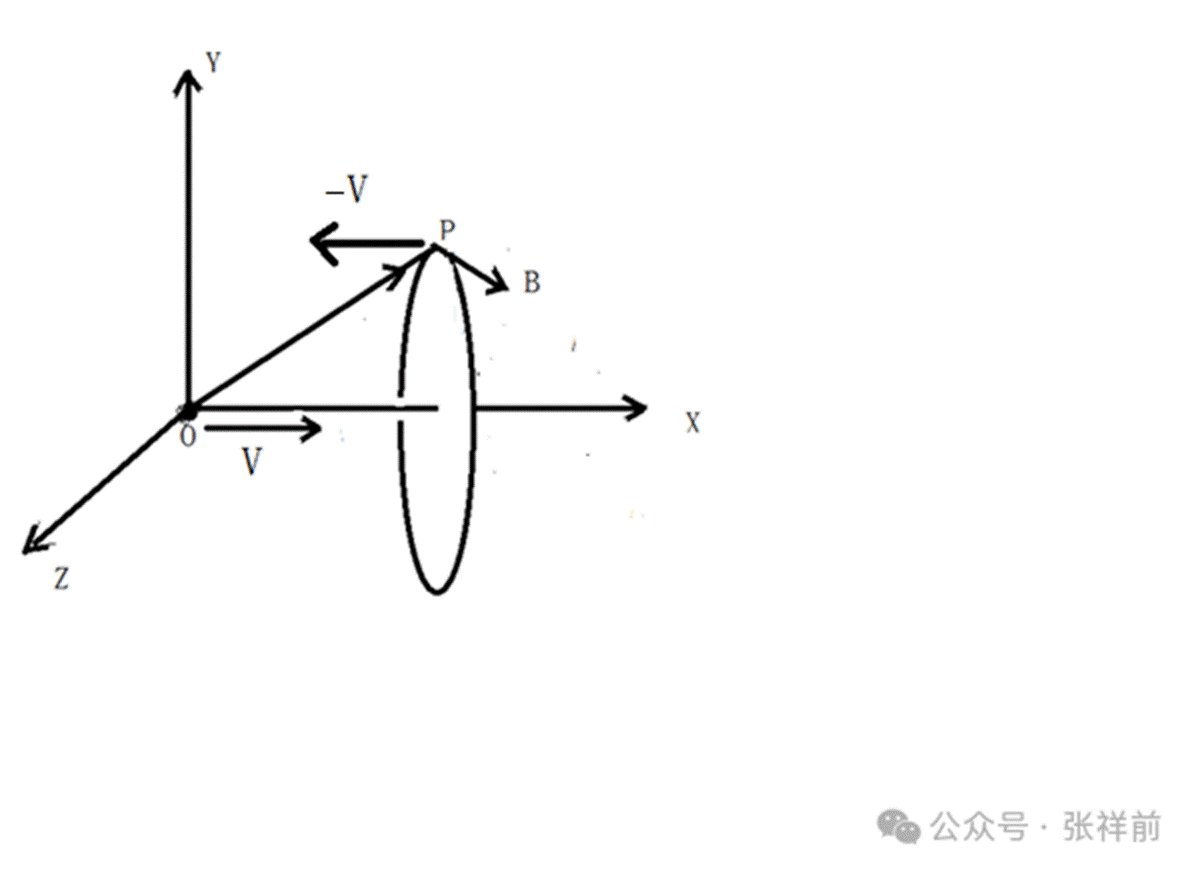
这个磁场的本质就是空间以矢量速度V为中心轴线在旋转，B的旋转和V满足右手螺旋关系。

B = V×E/c²

按照矢量叉乘和斯托克斯定理排列顺序的习惯，y叉乘以z形成了x方向上的矢量面元，z叉乘以x形成了沿y方向的矢量面元，x叉乘以y形成了沿z方向的矢量面元，三个分量满足以下右手螺旋关系：

Bx = 0

By = -V×Ez/c²

Bz = V×Ey/c²

o点是正电荷，Ez是o点产生的正电场沿z轴的分量，Ey是y轴上的分量。

o点产生的正电场由o点指向p点。

由前面的基本假设，o点以速度V沿x轴正方向运动的时候，空间点p正好有一个相反的速度﹣V。

如果我们把考察点从o点上移开，考察点设定在空间的p点上，则以上右手螺旋关系要改成左手螺旋关系：

Bx = 0

By = V×Ez/c²

Bz =﹣V×Ey/c²

当我们考察分析空间某处p点的运动情况，用这个分量公式更直接方便。

4，随时间变化的磁场产生电场和引力场

在统一场论中，引力场的旋度和均匀磁场所满足以下关系：

式中的f是常数。这个是磁场和引力场满足的基本关系方程，这个方程告诉我们，电荷以某一个速度匀速直线运动时候产生的磁场，可以表现为引力场的旋度形式。

电磁学和量子力学引入的磁矢势概念，并非是一个虚无的概念，其本质就是漩涡引力场。这个方程可能是量子力学中AB效应的最终解释。

将方程两边点乘矢量面元【可以看成是包围电荷粒子o点的高斯球面s = 4πr²上一小块面积，其正方向，也就是法方向向外】，再利用场论中的斯托克斯定理，可以得到磁场满足和引力场之间关系的积分方程：

这种引力场以磁力线为轴线，满足右手螺旋，在空间中环绕分布。

接下来，我们考虑磁场的变化情况。

设想一个正点电荷o点，在0时刻从笛卡尔坐标的原点出发，相对于我们观测者以速度【标量为v】沿x轴正方向匀速直线运动。

在参考系s系【s’系相对于s系以匀速度沿x轴正方向直线运动】里，点电荷o在周围空间点p处产生了电场、磁场，的环绕是右手螺旋。如下图。

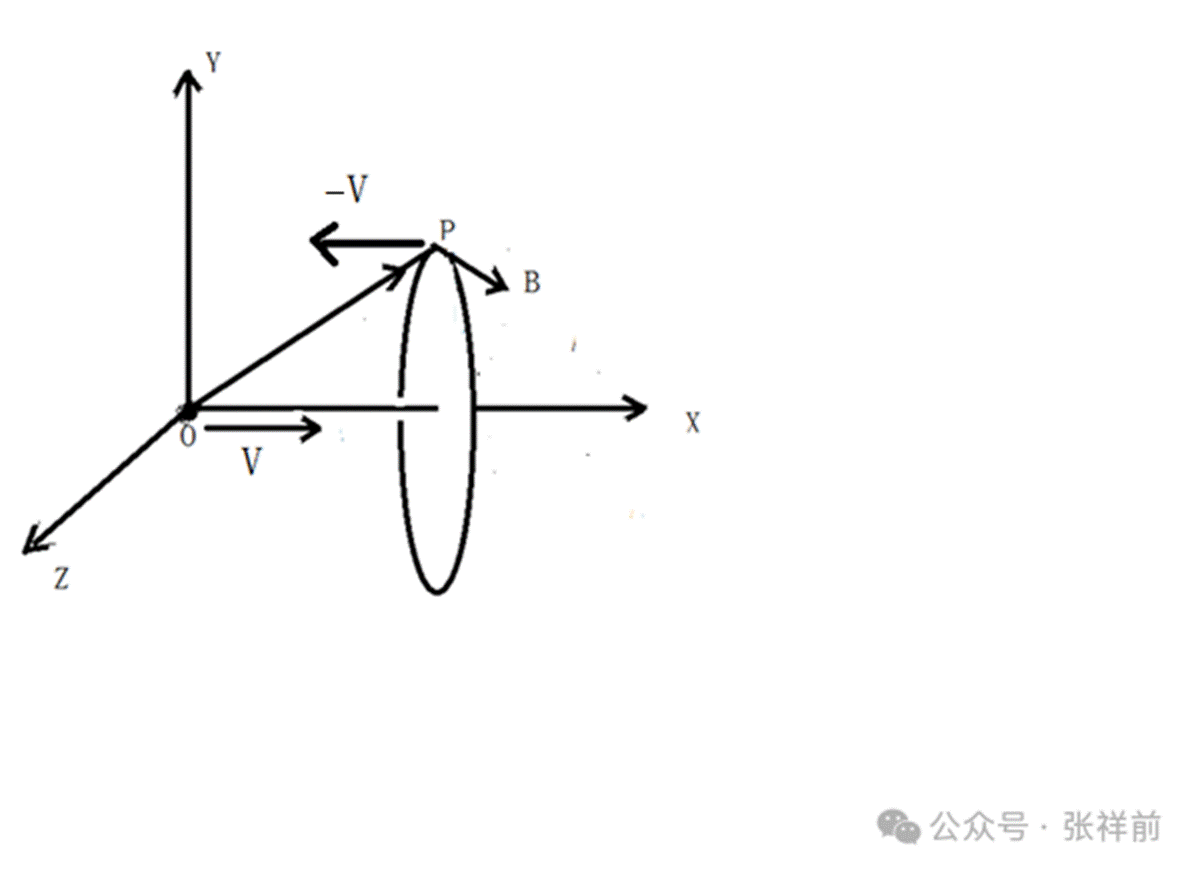
如果我们不以电荷o点作为考察点，而是以空间点p为考察点，由于o点的运动速度和p点的运动速度﹣ 方向正好相反，所以，这里的运动电场、均匀磁场满足左手螺旋关系式：

分量形式为：

将以上方程对时间t求导数，有：

如果我们能够证明表示的是磁场变化产生变化的电场【也称漩涡电场】，就是法拉第电磁感应原理，作为对应，多出的一项应该是变化磁场产生引力场。

因为是空间点p的加速度，按照统一场论的思想，空间本身的加速度等价于引力场。

我们先来证明就是法拉第电磁感应原理。

三个分量如下【微分号d改为偏微分号∂】：

由静电场旋度为零

和洛伦兹正变换中的

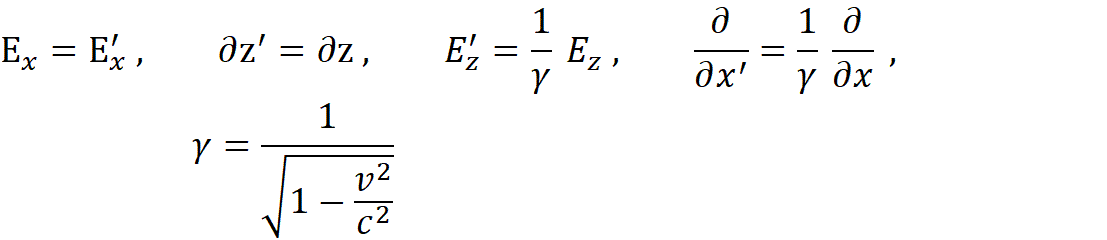
得到：

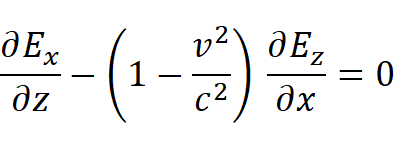
所以

由速度的定义得：

得到：

类似以上的操作，可以得到：

把这两个式子和上面的的三个分量：

对比，可以得到：

合并以上三式，正是法拉第电磁感应方程：

下面我们对磁场变化产生引力场的方程展开分析。

该方程的三个分量如下：

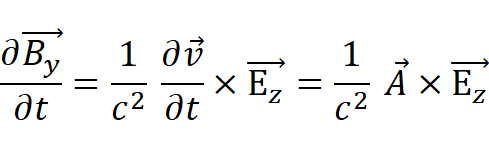
以上方程可以写为

对这个方程可以理解为：

磁场随时间t变化，可以产生电场和引力场，并且，在空间某一个点上，、、三者相互垂直，满足叉乘关系，构建了一个圆柱状螺旋式，统一场论中，场的本质就是以圆柱状螺旋式运动的空间。

磁场的本质就是空间以矢量速度V为中心轴线在旋转。

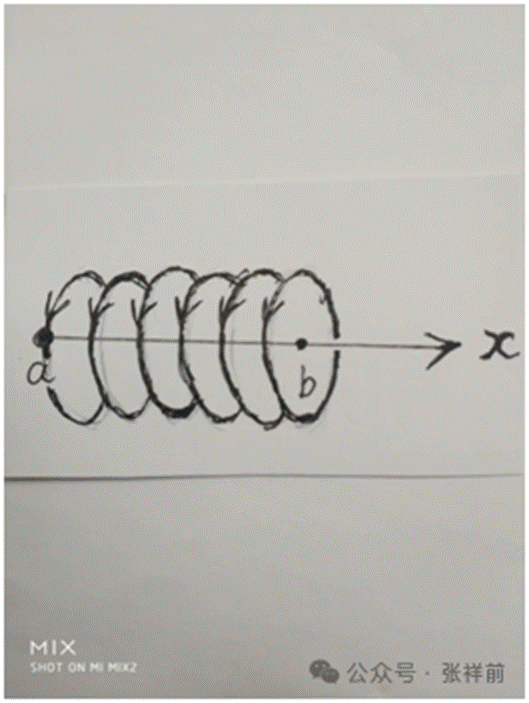
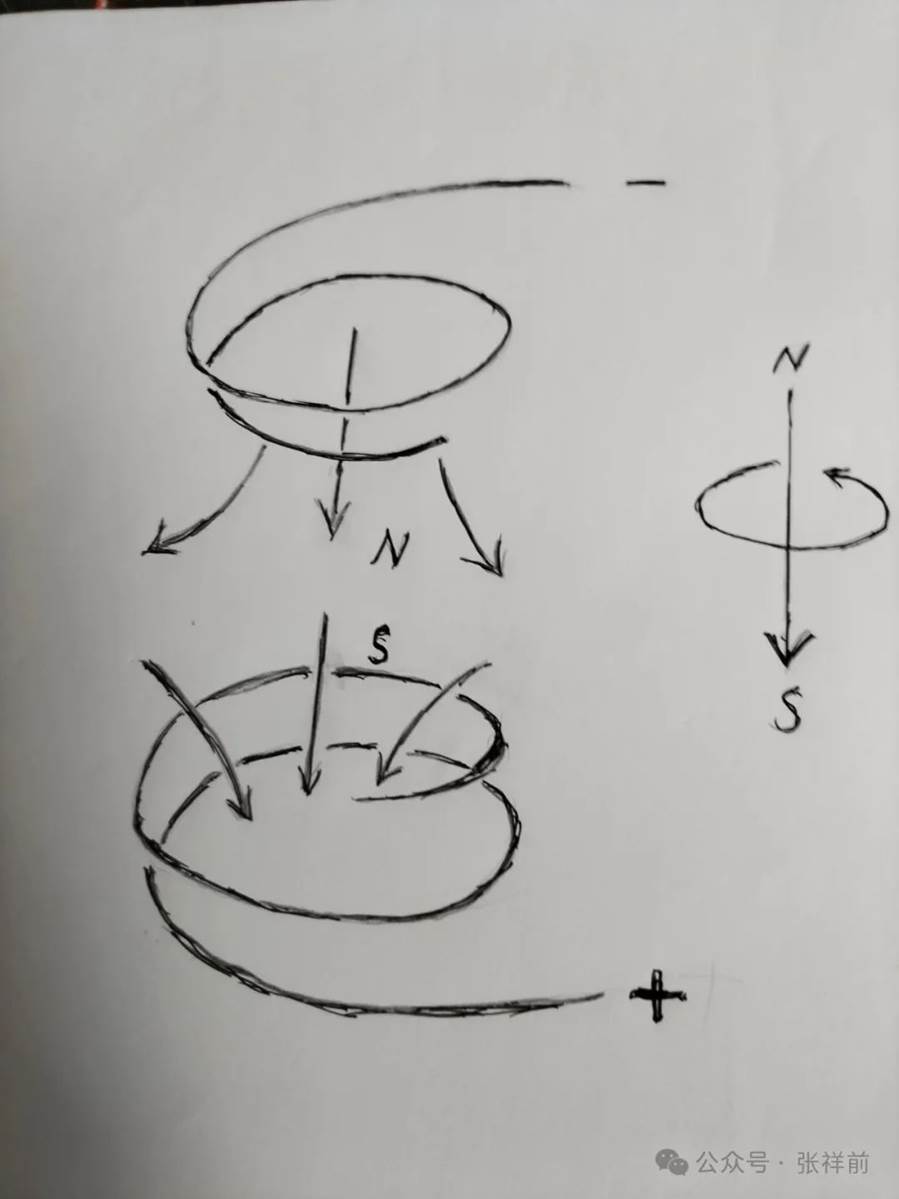
在上图中，从a点到b点是一条直线，磁场以圆柱状螺旋式环绕。

在下图中，从a点到b点是一个圆周的时候，空间的旋转运动在这个圆周的正反两个面上一进一出，进的一面是S极，出来的一面叫N极。

当导线是一条直线的时候，磁场是以导线为轴线环绕。当导线是一条圆周的时候，磁场仍然以圆周导线为轴线环绕。

在长直导线中，正电荷沿导线方向直线加速运动，产生了一个沿导线方向平行的引力场，这个引力场令物体沿导线平行方向加速直线运动。

我们可以设想，当导线弯曲成一个圆圈，物体沿圆圈导线运动，所以，会发生旋转。

在下图中：

根据右手定则，我们用右手握住导线，大拇指方向从正极指向负极，则四指环绕方向就是磁场的方向。

在上图中，悬挂物从负极向正极运动，所以，悬挂物以磁力线为轴线旋转，旋转满足左手螺旋。

从方程dB/dt=dV/dt×E/c²+(V×dE/dt)/c²来看：

(V×dE/dt)/c²表示的是磁场变化产生漩涡电场，也就是法拉第电磁感应原理。dB/dt=dV/dt×E/c²是磁场变化产生漩涡引力场。

既然磁场变化产生漩涡电场，满足左手螺旋。变化磁场产生漩涡引力场应该也是左手螺旋，因为dV/dt×E/c²和(V×dE/dt)/c²都是正号。

现在经过大量的试验，也证实了这一点。

由于变化电磁场产生引力场是统一场论的核心，也是人工场技术得以应用的关键。

下面，用另外一种方法来推导出加速振动正电荷产生加速度方向相反的引力场。

电场、磁场、引力场的各种关系，可以看成是磁场定义方程

B = V×E/c²这种基本关系的衍生，都可以从这个基本方程推导出来。

式dB/dt = A×E/c²只能适用于某些微观单个基本粒子，我们宏观看到的物体粒子，是许多微小带电粒子的复合，其正负电荷相互抵消了，磁场也有很多相互抵消了。

以上推导的变化磁场产生引力场公式dB/dt = A×E/c²有可能只适用于正电荷，因为正电荷周围空间光速发散运动，可以把空间的扭曲效应【包含了加速电场、加速磁场和变化电场形成的引力场】以光速发散出去。

而负电荷周围空间光速向内收敛运动，按理是不能把空间扭曲效应发散出去的。但是，按照洛伦茨变换，光速运动空间缩短为零，不再和我们是同一个空间，对我们观察者来说无法观察，有不确定性。所以，这个公式能不能适用负电荷，还需要理论进一步探讨和实践去判断。

为了进一步搞清楚加速运动电荷的电场、磁场、引力场三者之间的关系，我们结合一个实例来展开分析。

设想一个相对于我们观测者静止的点电荷o，带有电量为q的正电荷，在周围空间点p处产生了静电场E。

在零时刻，当o点突然相对于我们以矢量加速度G【数量为g】沿x轴正方向加速运动。

按照统一场论，o点的加速度运动，会导致空间点p从o点出来，以矢量光速C向外运动的同时，叠加了一个加速度-G。

按照统一场论的引力场定义——引力场是空间点本身的加速度运动，引力场A【数量为a】和空间点p的加速度-G是等价的，所以，空间点p所在的位置，会因为o点的加速度运动产生一个引力场：

A【数量为a】=–G。

我们来求出静电场Er、加速变化的扭曲电场Eθ、引力场A之间的关系。

设想正点电荷o相对于我们观测者一直静止在笛卡尔坐标系的原点o，从时刻t = 0开始以加速度G【数量为g】沿x轴正方向作直线匀加速度运动。

在时刻t =τ时，o点到达了d点就停止加速运动，此时的速度达到了v = gτ，以后就以速度v继续沿x轴作匀速直线运动，一直运动到后来的q点。

如下图所示：

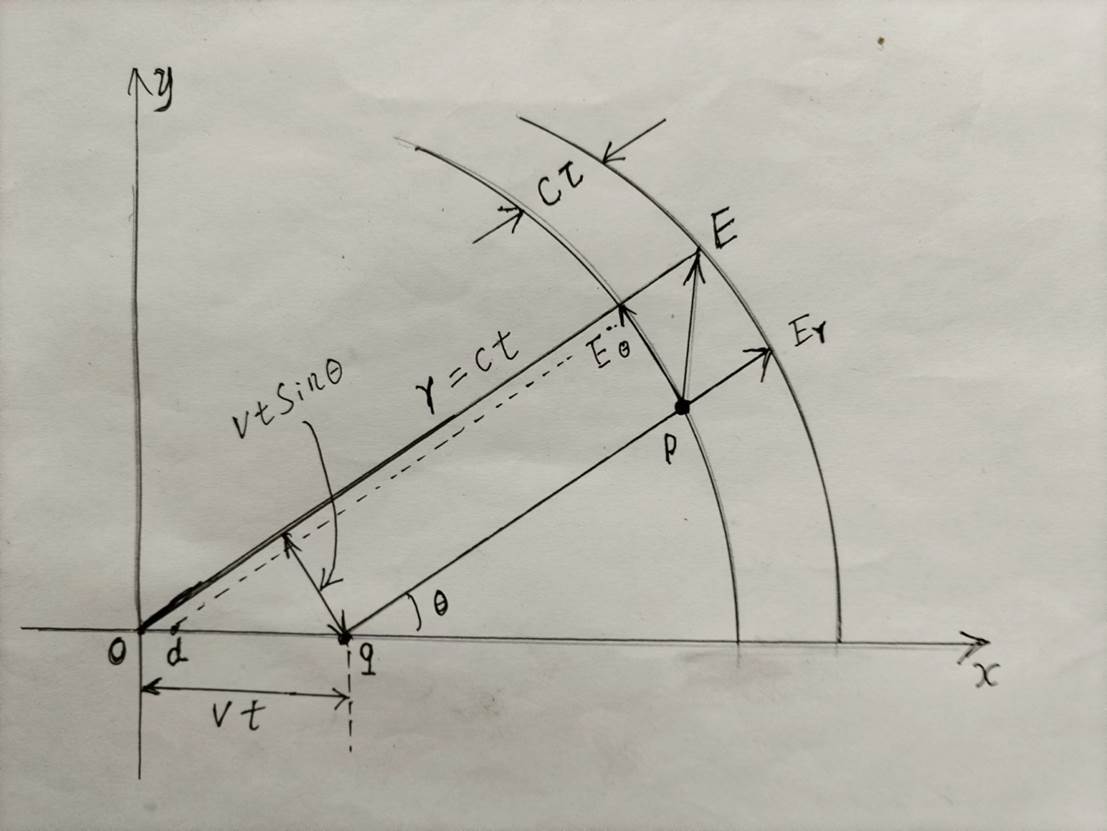
为了简单起见，我们考虑的是v远远小于光速c，od距离远小于oq。

下面我们考虑在任意时刻t (t远大于τ)时电荷o周围的电场分布情况。

在0时刻至τ时刻这一段时间内，由于正点电荷o的加速运动使它周围的电场线发生扭曲，并且这个扭曲状态也会以光速c向外延伸。

统一场论明确的指出，正电荷的电场线就是电荷周围以光速运动的空间点运动位移。

以上的扭曲状态以光速向外运动，就像一个向四周匀速喷水的水龙头，一旦水龙头抖动一下，引起水流发生扭曲，这个扭曲状态肯定的是以水流的速度向外延伸。

由加速运动电荷o引起的电场的扭曲状态以光速c向外延伸，在上图中可以看到扭曲状态的厚度为cτ，夹在两个球面之间。

后一个球面，在t时刻已向四周传播了c（t-τ）这么远的距离，这个球面是以q点为中心，直径为c（t-τ）的球面。

前一个球面，在t时刻已向四周传播了ct这么远的距离，这个球面是以o点为中心，直径为ct的球面。

由于从时刻t=τ开始，电荷o作匀速运动，所以在这个直径为c（t-τ）的球面内分布的电场应该是作匀速直线运动电荷的电场。

根据我们前面的设定，电荷o的运动速度v远远的小于光速c,所以这球面内的电场在任意时刻都近似为静电场。

在时刻t这一电场的电场线是从此时刻o点所在位置q引出的沿半径方向的直线。

由于t远大于τ，c远大于v，所以r=ct远大于vτ/2(即从o点到d点的距离)。因此，扭曲状态的前、后沿的两个球面几乎是同心圆。

随着时间的推移，以上的扭曲状态的半径（ct）不断的扩大，以光速向外延伸、传播。

我们从统一场论中电荷、电场定义方程知道，电场线发生扭曲，不会改变电场线的条数，仍然是连续的，所以在扭曲状态的前后两侧面的电场线的条数是相等的。

在v远小于c时候，这个扭曲的电场线可以当直线来看待。

我们选用与x轴成θ角的那一条电场线来分析。

由于从o点到d点的距离od相比r = ct要小得多，我们可以把o点和d点看作为一点(也就是od接近于零)。

而oq =vτ/2+v(t-τ)≈vt

扭曲区内的电场E可以分成两个分量Er【径向电场，电荷静止时候本来就存在，其数量为er，】和Eθ【横向电场，可以看成是Er的变化形式，其数量为eθ】。

由上图可以看出

eθ/er= vt sinθ/cτ= g t sinθ/c = g r sinθ/c²

在统一场论中，引力场的本质就是空间点的加速度，但是，引力场与引力场源指向引力场点p的位置矢量R【数量为r】方向相反。

所以，这里的引力场可以用A【数量为a = -g】表示，所以有：

Eθ/er = A×R/c²

上式中由o点指向空间点p的位置r =ct改用矢量R来表示。

以上电场Eθ垂直于电磁场的传播方向（这里是Er的方向），并且只有在扭曲状态中存在。所以，它就是电荷o点加速运动时候所产生的横向扭曲电场。

Eθ可以看成是电荷因为加速运动引起了Er的变化。

上式给出了电荷o静止时候本来就存在的电场Er、加速运动引起Er的变化形式Eθ、加速运动电荷o产生的引力场A三者之间的关系。

接下来，我们求出加速运动点电荷周围的变化磁场和产生的引力场之间的关系。

按照麦克斯韦方程，电场在真空中变化，必然产生变化的磁场。

统一场论、相对论都认为，电荷o以速度V运动的时候，电场E和磁场B满足一种基本关系：

B = V×E/ c²

由电荷加速运动而变化产生的横向电场Eθ、横向磁场Bθ【数量为bθ】所满足的关系，没有跳出B =V×E/ c²。

只是这个时候，运动速度V不是电荷的运动速度，而是电荷周围空间点p【也可以说是场点，考察点】的运动速度。

统一场论指出，静止物体周围任意一个空间点以矢量光速C’向四周发散运动，当物体以速度V匀速直线运动的时候，空间点的运动速度变为C-V，所以，空间点本来的矢量光速C’和C比较有了一个改变量——速度V。

但是，这里的电荷运动速度远远小于光速，所以，空间点p 的速度仍然可以看成是矢量光速C。

由于扭曲状态是以光速在传播，加上统一场论的矢量光速概念，所以，空间点的运动速度是矢量光速C，因此有式：

Bθ= C×Eθ/ c²

数量形式为：

c bθ= eθ

把上式和式Eθ/er = A×R/c²【注意，er是Er的数量】比较，我们有：

Bθ/er= A×R/c³

上式表示了电荷静止时候就存在的电场Er【数量为er】因为电荷加速运动而变化，所产生的引力场A、变化磁场Bθ三者之间的关系。

利用时空同一化方程R=Ct，上式Bθ/er= A×R/c³也可以改写为：

Bθ= er(A×【R】)t/c²

【R】是矢量R的单位矢量，和C的方向一致，er的方向和【R】也是一致，所以，

er【R】= Er

所以，有：

Bθ= (A×Er)t/c²

将以上两边对时间t求导数，得：

dBθ/dt = A×Er/c²

其实，这个公式，和前面的磁场定义方程B= V×E/c²对时间t求导数：

dB/dt =(dV/dt)×E/c²= A×E/c²

是吻合的，用语言描述就是：

加速运动正电荷在周围空间产生加速度方向相反的引力场，并以光速向西周扩散传播。

可以看出，变化电磁场产生变化电场和引力场方程，没有跳出磁场和电场满足的基本关系方程B = V×E/c²，电场、磁场、引力场的一切关系都是这个方程的变种而已。

以上描述了正电荷加速运动，引起电场变化，产生了变化磁场和引力场，并且给出了加速变化电场、加速变化磁场、引力场三者相互关系【包含了方向】。

【附录】变化电磁场产生引力场试验的理论推导【可以复制的数学公式】。

以下是变化电磁场产生引力场的理论推导过程。详细的推导过程见《统一场论》，加本人微信可以获得《统一场论》电子版资料。

1，基本假设

宇宙任何物体，周围空间总是以矢量光速C’【本文大写字母为矢量】、以圆柱状螺旋式向四周发散运动。

在统一场论中，圆柱状螺旋式运动的直线运动部分是电场，旋转运动部分是磁场，旋转指向中心轴线的加速度是引力场。

三场相互垂直。

静止物体周围也有磁场，只是在一个曲面上多少磁场线穿进去，就有多少磁场线穿出来，相互抵消了，对外不显效应。

以上基本假设提到了空间本身在运动。

为了描述空间本身的运动，我们把空间分割成许多个小块，每一个小块叫空间点，通过描述空间点的运动，就可以描述空间本身的运动。

以上基本假设提到了矢量光速。

本文认为光速可以扩展到矢量，矢量光速的方向可以变化，模是标量光速，用小写字母c表示，c不变。

C’和C大小相等，方向不同。C’和C的关系是否符合相对论的洛伦茨变换？

按照洛伦茨的速度变换，C’的三个分量Cx’，Cy’， Cz’和C的三个分量Cx，Cy，Cz满足的关系为：

Cx’ = (Cx – v)/[1- (Cx v/c²)]

Cy’ = [Cy√（1-v²/c²）]/ [1- (Cx v/c²)]

Cz’ = [Cz√（1-v²/c²）]/ [1- (Cx v/c²)]

由以上可以导出：

（Cx’）²+（Cy’）²+（Cy’）²

= [(Cx– v)²+ Cy²（1-v²/c²） + Cz²（1-v²/c²） ]/[1- (Cx v/c²)]²

= c²c²[Cx²+ Cy²+ Cz²-2 Cx v+ v²-（c²-Cx²）v²/c²]/（c²-Cx v)²

= c²c²[c²-2 Cx v+ v²-（c²-Cx²）v²/c²]/（c²-Cx v)²

= c²[c²c²-2 c²Cx v+ Cx²v²]/（c²-Cx v)²

= c²

由此导出矢量光速C和C’满足以下关系：

C’·C’ = C·C = c²

C和C’方向不一样，但是，数量是一样的。

当o点相对于我们观察者以速度V运动的时候，设p点相对于o点的速度为U，由于C是U和V的合成，也就是C=U+V，

所以：

U=C-V

2，认识引力场

我们站在地球上，随手放下一块石头，石头以加速度自由落体向地球中心坠落。

如果没有石头，石头所在的空间仍然以那种方式在向地球中心坠落。这个就是引力场的本质。

引力场的本质就是物体周围空间本身向物体加速运动的加速度。

引力场有两个重要的性质：

由物体指向引力场中的一点【我们叫场点，或者叫考察点】的位置矢量，与引力场方向相反。

引力场可以对一切材料构成的物体有加速作用。

3，认识磁场

这个磁场的本质就是空间以矢量速度V为中心轴线在旋转，B的旋转和V满足右手螺旋关系。

B = V×E/c²

Bx = 0

By = -V×Ez/c²

Bz = V×Ey/c²

o点是正电荷，Ez是o点产生的正电场沿z轴的分量，Ey是y轴上的分量。

o点产生的正电场由o点指向p点。

由前面的基本假设，o点以速度V沿x轴正方向运动的时候，在p点正好有一个相反的速度-V。

如果我们考察点设定在p点，则以上右手螺旋关系要改成左手螺旋关系：

Bx = 0

By = V×Ez/c²

Bz =﹣V×Ey/c²

当我们考察分析空间某处p点的运动情况，用这个分量公式更直接方便。

4，随时间变化的磁场产生电场和引力场

设想一个点电荷o点，在0时刻从原点出发，相对于我们观测者以匀速度V【标量为v】沿x轴正方向匀速直线运动，o点在周围任意一个空间点p处产生了运动电场E、均匀磁场B：

B= V×E/c²

当o点相对于我们以加速度-A沿x轴正方向运动，电荷o在周围任意一个空间点p处产生了运动电场E、非恒稳磁场dB/dt 和引力场 A。

我们以空间某处p点为考察点，将磁场定义方程B= V×E/c²对时间t求导数，有：

dB/dt=dV/dt×E/c²+(V×dE/dt)/c²

如果我们能够证明dB/dt= (V×dE/dt)/c²表示的是：

磁场变化产生变化的电场【又称漩涡电场】，也就是法拉第电磁感应原理，作为对应，dB/dt=dV/dt×E/c²应该是变化磁场产生引力场。

因为dV/dt=A是空间点p的加速度，按照前面我们对引力场的认识，空间本身的加速度等价于引力场。

我们首先证明dB/dt= (V×dE/dt)/c²就是法拉第电磁感应原理。

由于考察点不再粒子o点上，而在空间点p上，所以，磁场B和电场E的关系，我们采用左手螺旋式：

Bx = 0

By =（v/c²）Ez

Bz = -（v/c²）Ey

dB/dt= (V×dE/dt)/c²的三个分量如下【微分号改为偏微分号】：

∂Bx/∂t = 0

∂By/∂t =（v ∂Ez/∂t）/c²

∂Bz/∂t = -（v ∂Ey/∂t）/c²

由静电场旋度为零∂Ex’/∂z’ - ∂Ez’/∂x’=0，和洛伦茨正变换中的Ex= Ex’，∂z’ =∂z，γEz’= Ez，∂/γ∂x=∂/∂x’，γ=1/√（1- v²/c²），得到：

∂Ex/∂z–（1/γ²）∂Ez/∂x = 0

∂Ex/∂z–（1- v²/c²）∂Ez/∂x = 0

∂Ex/∂z–∂Ez/∂x = -（v²/c²）∂Ez/∂x

由速度定义dv/dt=v, 得到v ∂/∂x = ∂/ ∂t，所以：

∂Ex/∂z–∂Ez/∂x = -（v/c²）∂Ez/∂t

由静电场旋度为零∂Ey’/∂x’ - ∂Ex’/∂y’=0，和洛伦茨正变换中的Ex= Ex’，∂z’ =∂z，γEy’= Ey，∂/γ∂x=∂/∂x’，γ=1/√（1- v²/c²），得到：

（1/γ²）∂Ey/∂x –∂Ex/∂y = 0

∂Ey/∂x–∂Ex/∂y- (v²/c²）∂Ey∂x = 0

由dv/dt=v, 得到v ∂/∂x = ∂/ ∂t，所以：

∂Ey/∂x–∂Ex/∂y = （v/c²）∂Ey/∂t

把这两个式子和上面的dB/dt= (V×dE/dt)/c²的三个分量：

∂Bx/∂t = 0

∂By/∂t =（v ∂Ez/∂t）/c²

∂Bz/∂t = -（v ∂Ey/∂t）/c²

对比，可以得到：

∂Ez/∂y–∂Ey/∂z = 0

∂Ex/∂z–∂Ez/∂x = - ∂By/∂t

∂Ey/∂x–∂Ex/∂y = - ∂Bz/∂t

合并以上三式，正是法拉第电磁感应方程：

∇×E= - ∂B/∂t

下面我们对磁场B变化产生引力场A方程dB/dt=（dV/dt）×E/c²展开分析。

该方程的三个分量如下：

∂Bx/∂t = 0

∂By/∂t =（∂V/∂t） ×Ez/c²=A ×Ez/c²

∂Bz/∂t = -（∂V/∂t） ×Ey/c²= - A×Ey/c²

微分号d已经改成了偏微分号∂。其中A的方向是空间点p的加速度方向，和x轴正方向相反。

以上方程可以写为dB/dt=A×E/c²，对这个方程可以理解为：

正电荷o点沿x轴正方向加速运动的时候，在周围空间任意一点p处，产生了变化的磁场dB/dt、电场E和沿加速度方向相反的引力场A。

A、E、dB/dt三者相互垂直，满足叉乘关系，构建了一个圆柱状螺旋式，统一场论中，场的本质就是以圆柱状螺旋式运动的空间。

这个就是我们第一个试验——加速运动正电荷产生加速度方向相反的直线引力场的理论解释。

对于磁场变化产生漩涡引力场，基本原理和以上是一样的。

磁场的本质就是空间以矢量速度V为中心轴线在旋转。

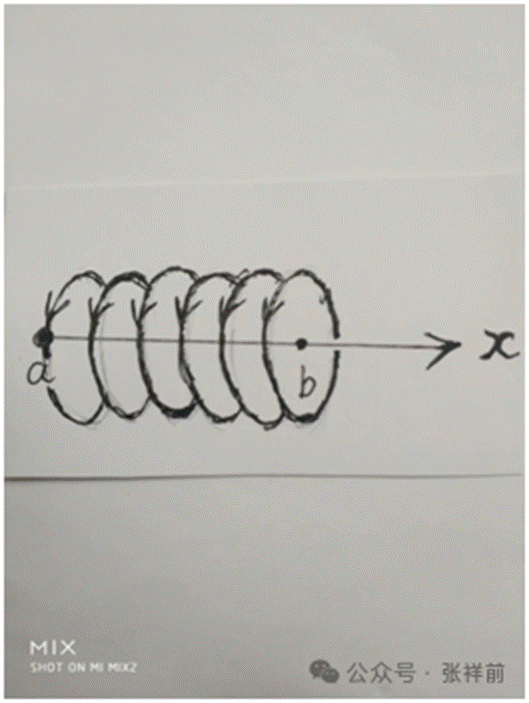
在上图中，从a点到b点是一条直线，磁场以圆柱状螺旋式环绕。

在下图中，从a点到b点是一个圆周的时候，空间的旋转运动在这个圆周的正反两个面上一进一出，进的一面是S极，出来的一面叫N极。

当导线是一条直线的时候，磁场是以导线为轴线环绕。当导线是一条圆周的时候，磁场仍然以圆周导线为轴线环绕。

在长直导线中，正电荷沿导线方向直线加速运动，产生了一个沿导线方向平行的引力场，这个引力场令物体沿导线平行方向加速直线运动。

我们可以设想，当导线弯曲成一个圆圈，物体沿圆圈导线运动，所以，会发生旋转。

在下图中：

根据右手定则，我们用右手握住导线，大拇指方向从正极指向负极，则四指环绕方向就是磁场的方向。

在上图中，悬挂物从负极向正极运动，所以，悬挂物以磁力线为轴线旋转，旋转满足左手螺旋。

从方程dB/dt=dV/dt×E/c²+(V×dE/dt)/c²来看：

(V×dE/dt)/c²表示的是磁场变化产生漩涡电场，也就是法拉第电磁感应原理。dB/dt=dV/dt×E/c²是磁场变化产生漩涡引力场。

既然磁场变化产生漩涡电场，满足左手螺旋。变化磁场产生漩涡引力场应该也是左手螺旋，因为dV/dt×E/c²和(V×dE/dt)/c²都是正号。

现在经过大量的试验，也证实了这一点。

徐玉川低电压磁场变化产生引力试验---徐氏试验

2024年12月02日 18:15

作者张祥前交流微信18714815159

2024年9月25日，安徽迪维乐普非晶器材有限公司的老总徐玉川，在我的理论指导下，在12伏至160伏低电压情况下，试验发现了磁场变化产生明显的引力场效应，这是自1831年法拉第发现电磁感应以来，人类最重大的科学发现，表明取代电文明的场文明时代已经到来。

我们暂且把这个试验叫“徐玉川低电压磁场变化产生引力试验”，简称徐氏试验，所产生的效应叫徐氏效应。

徐总这个试验已经向国家专利局提交了申请，前一段时间，国家专利局的受理书已经下来了。

我们现在已经联系了一些视频博主和网友，我也准备发动我的粉丝，长期在海内外宣传徐氏试验。努力的把反重力试验爱好者转向徐氏试验上。

为什么要把变化电磁场产生引力场试验选择在徐氏试验作为突破口？是以下几个因素考量。

1，徐氏试验简单可靠，稳定性好，每次都能够试验成功，适合网友复刻。

2，12至160伏低电压，可以摆脱离子风、静电马达效应的干扰，不像我的试验都是几万伏。

3，徐氏试验成本低，2千元就可以搞定，又很安全，适合广大网友和爱好者复刻。适合大规模宣传传播。

4，徐氏试验有成熟的统一场论理论解释和数学方程描述。

5，徐氏试验还可以升级，给了喜欢挑战的网友极大兴趣。

6，徐氏试验最终可以使场能量取代电能，特别是在医疗领域的应用，隐含了百万亿人民币经济规模。

我以前把详细的试验方法公布了，徐总又把把试验用的关键的非晶纳米材料【如下图】

图片

送到我的住处。

想重复这个试验的网友、高校、科研所，联系我可以获得非晶材料以及变化电磁场产生引力场的理论推导过程。

其他的试验材料，淘宝上很容易买到。这个试验简单，而且成本可以控制在2千元内。

试验方法：

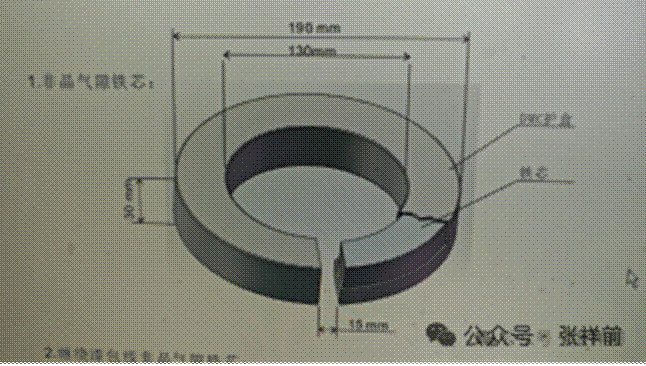
选用非晶材质的软磁环形铁芯，在圆环上切开一个15 mm长度的切口，形成一段长15 mm的气隙。

图片

该非晶材料饱和磁感应强度Bs = 1.25特斯拉（T），磁导率大于等于100000，铁芯内径130 mm，外径190 mm，厚度30 mm。

在圆环上用直径2mm的漆包铜线绕制400匝的励磁绕组。

图片

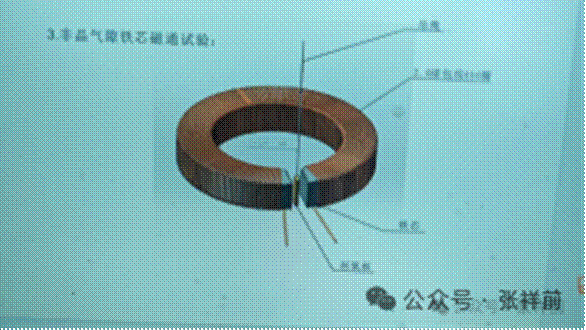
线圈通电后，发现可使一切材质的物体发生运动，运动的方向明显与磁力线垂直。

在气隙处，沿磁力线的一个垂直剖面上，取这个剖面的中心点，放置在气隙处的一切材料物体，沿磁力线垂直方向，向这个中心点运动。

这种运动和地球表面产生的引力场令一切物体运动高度类似，我们有理由相信是变化的电磁场产生了引力场。

我们使用电流30 A、频率50 Hz、电压80伏的交流电试验过，还用12V至80V、30A至300A直流电进行过试验，和交流电的情况类似。

直流电源可以用5个20安时电瓶车电瓶串联【电压为64伏左右】，也可以用交流转直流电源。也可以用315A逆变电焊机等。

也可以用调压器加交流转直流的逆变器作为电源。

气隙处磁场峰值强度，经过检测约为0.1至0.3特斯拉（T）。

在气隙处用细线悬挂的试验材料有：

1，环氧树脂板（强绝缘材料）；2，陶瓷；3，塑料；4，不锈钢；5，绿色树叶；6，生鲜的猪肉；7，聚乙烯；8，铝；9，橡胶；10，纸；11，玻璃；12，铜；13，有机玻璃，14，水平仪里面的玻璃管和气泡······等其他材料。

复刻徐氏试验的网友，如果在试验过程中，有什么疑问的，可以微信上咨询我。试验注意悬挂物不能贴上线圈。切口不能太大。

有人说这个试验效应是抗磁性。

不同的材料抗磁性不一样，有的还是顺磁性，试验中发现产生的磁场不强，换几十种不同的材料试验，包括了烟雾、液滴、水中的气泡，都发现相同的运动形式，这个是抗磁性无法解释的。

至于有人说是离子风和静电马达效应，这个12v---160v低电压情况下，是不可能有的。

Theoretical Deduction Process of Gravitational Field Produced by Changing Electromagnetic Field

Zhang Xiangqian Occupation: Farmer, repairing bicycles May 29, 2024

1 Basic Assumptions

Any object in the universe, the surrounding space always moves in a cylindrical spiral with the vector speed of light C⃗ ′ . The linear motion part of cylindrical spiral motion is electric ffeld, the rotating motion part is magnetic ffeld, and the acceleration pointing to the central axis is gravitational ffeld. The three ffelds are perpendicular to each other. There is also a magnetic ffeld around a stationary object, but as many magnetic ffeld lines pass through a curved surface, so many magnetic ffeld lines pass through, which cancel each other out and have no external effect. The above basic assumptions mentioned that space itself is moving. In order to describe the motion of the space itself, we divide the space into many small pieces, each of which is called a space point. By describing the motion of the space point, we can describe the motion of the space itself. The above basic assumptions mentioned the vector speed of light. This paper holds that the speed of light can be extended to vector, the direction of vector speed of light can be changed, and the module is scalar speed of light, which is represented by lowercase letter c, and c is unchanged. When the object particle point O is stationary relative to our observer, a space point P around it diverges around at the vector light speed C⃗ ′ , and when the point O moves relative to us at the speed ⃗v, the speed of the point P

relative to our observer is expressed by the vector light speed ⃗c. C⃗ ′ and ⃗c are equal in size but different in direction. Does the relationship between C⃗ ′ and

⃗c conform to the Lorentz transformation of relativity? According to Lorenz’s velocity transformation, the three components C ′ x , C ′ y , C ′ z of C⃗ ′ and the three 1components Cx, Cy, Cz of C⃗ satisfy the following relationship:

C ′ x = Cx − v

1 − Cxv c 2

C ′ y = Cy

1 − v 2

c 2

1 − Cxv c 2

C ′ z = Cz

1 − v 2

c 2

1 − Cxv c 2

It can be derived from the above: (C ′ x ) 2 + (C ′ y ) 2 + (C ′ z ) 2 = (Cx − v) 2 + C 2 y (1 − v 2

c 2 ) + C 2 z (1 − v 2

c 2 ) (1 − Cxv c 2 ) 2

= c 2 c 2 [C 2 x + C 2 y + C 2 z − 2Cxv + v 2 − (c 2 − C 2 x ) v 2

c 2 ] (c 2 − Cxv) 2

= c 2 c 2 [c 2 − 2Cxv + v 2 − (c 2 − C 2 x ) v 2

c 2 ] (c 2 − Cxv) 2

= c 2 c 2 c 2 − 2c 2Cxv + C 2 x v 2

(c 2 − Cxv) 2

= c 2

The vector light velocities ⃗c and C⃗ ′ derived from this satisfy the following relationship:

C⃗ ′ · C⃗ ′ = C⃗ · C⃗ = c 2

C⃗ and C⃗ ′ are in different directions, but the quantity is the same. When point

O moves at a speed V⃗ relative to our observer, let the speed of point P relative to point O be U⃗ , because C⃗ is the composition of U⃗ and V⃗ , that is, C⃗ = U⃗ + V⃗ , So:

U⃗ = C⃗ − V⃗

2 Understanding the Gravitational Field

We stood on the earth and put down a stone casually. The stone fell freely to the center of the earth at an acceleration. If there were no stones, the space where the stones were located would still be falling towards the center of the earth in that way. The essence of gravitational ffeld is the acceleration of the space around the object itself to accelerate the movement of the object. The gravitational ffeld has two important properties:

The position vector from an object to a point in the gravitational ffeld [we call it a ffeld point or an investigation point] is opposite to the gravitational ffeld.

The gravitational ffeld can accelerate the objects made of all materials. 2

3 Understanding the Magnetic Field

It is found that charged particles move in a straight line at a uniform speed relative to our observers, which causes the electric ffeld change in the vertical direction of the movement speed. The electric ffeld change part can be considered as a magnetic ffeld, that is, the electric ffeld that changes with the speed produces a magnetic ffeld. In the ffgure below, an electrostatic ffeld E⃗ ′ is generated at the surrounding space point P at a point O of positively charged particles that is stationary relative to us. When point O moves in a straight line at a uniform speed V⃗ along the positive direction of the X axis relative to our observer, a magnetic ffeld B⃗ can be generated. The essence of this magnetic ffeld is that the space is rotating with the vector velocity ⃗v as the central axis, and the rotation of B⃗ and V⃗ satisfy the right-handed spiral relationship.

B⃗ = V⃗ × E⃗ c 2

According to the habit of vector cross multiplication and Stokes theorem arrangement order, Y cross multiplied by z forms a vector bin in the X direction, Z cross multiplied by x forms a vector bin in the Y direction, and X cross multiplied by y forms a vector bin in the Z direction. The three components satisfy the following right-handed spiral relationship:

Bx = 0

By = − V⃗ × Ez

c 2

Bz = V⃗ × Ey

c 2

Point O is a positive charge, Ez is the component of the positive electric ffeld generated by point O along the z axis, and Ey is the component on the y axis. The positive electric ffeld generated by point O points from point O to point

P. According to the previous basic assumption, when point O moves along the positive direction of X axis with speed V⃗ , there is just an opposite speed −V⃗

at point P. If we set the inspection point at point P, the above right-handed spiral relationship should be changed to left-handed spiral relationship:

Bx = 0

By = V⃗ × Ez

c 2

Bz = − V⃗ × Ey

c 2

It is more direct and convenient to use this component formula when we investigate and analyze the movement of point P somewhere in space. 3

4 Time-varying Magnetic Fields Produce Electric and Gravitational Fields

Imagine a point charge O, starting from the origin at time 0, moving in a straight line along the positive direction of the X axis at a uniform speed V⃗ [scalar is

V ] relative to our observer, and the point O generates a moving electric ffeld E⃗

and a uniform magnetic ffeld B⃗ at any surrounding space point P:

B⃗ = V⃗ × E⃗ c 2

When point O moves along the positive direction of X axis with an acceleration

−A⃗ relative to us, the electric charge O generates a moving electric ffeld E⃗ , an uneven magnetic ffeld dB⃗ dt and a gravitational ffeld at any space point P around it. Let’s take point P somewhere in space as the investigation point, and take the derivative of the magnetic ffeld deffnition equation B⃗ = V⃗ ×E⃗ c 2 to time t, which is as follows:

dB⃗ dt = dV⃗ dt × E⃗ c 2 + V⃗ × dE⃗ dtc 2

If we can prove that V⃗ × dE⃗ dtc 2 means: The change of magnetic ffeld produces a changing electric ffeld [also called eddy electric ffeld], which is Faraday electromagnetic induction principle. As a corresponding, dV⃗ dt × E⃗ c 2 should be a gravitational ffeld produced by changing magnetic ffeld. Because dV⃗ dt = A⃗ is the acceleration of space point P, according to our previous understanding of the gravitational ffeld, the acceleration of space itself is equivalent to the gravitational ffeld. We ffrst prove that V⃗ × dE⃗ dtc 2 is Faraday’s electromagnetic induction principle. Because the investigation point is not on the O point, but on the space point P, we adopt the left-handed spiral for the relationship between the magnetic ffeld B⃗ and the electric ffeld E⃗ :

Bx = 0

By = ⃗v c 2 Ez

Bz = − ⃗v c 2 Ey

The three components of dB⃗ dt = V⃗ × dE⃗ dtc 2 are as follows: [The differential sign is changed to the partial differential sign]

∂Bx

∂t = 0

∂By

∂t = v c 2

∂Ez

∂t ∂Bz

∂t = − v c 2

∂Ey

∂t

4From the fact that the curl of electrostatic ffeld is zero ∂E ′

∂x′ − ∂E ′

∂y′ = 0, and Ex =

E′ x , ∂z ′

∂z , γE′ z = Ez, ∂ γ∂x = ∂ ∂x′ , γ = q 1 1− v2

in Lorentz positive transformation, we get:

v ∂Ex

∂z − 1

γ 2

∂Ez

∂x = 0 ∂Ex

∂z − (1 − v 2

c 2 ) ∂Ez

∂x = 0 ∂Ex

∂z − ∂Ez

∂x = − v 2

c 2

∂Ez

∂x

From dv dt = v, v ∂ ∂x = ∂ ∂t is obtained, so:

∂Ex

∂z − ∂Ez

∂x = − v c 2

∂Ez

∂t

From the fact that the curl of electrostatic ffeld is zero ∂E ′

∂x′ − ∂E ′

∂y′ = 0, and Ex =

E′ x , ∂z ′

∂z , γE′ y = Ey, ∂ γ∂x = ∂ ∂x′ , γ = q 1 1− v2

in Lorentz positive transformation, we get: 1

γ 2

∂Ey

∂x − ∂Ex

∂y = 0 ∂Ey

∂x − ∂Ex

∂y − v 2

c 2

∂Ey

∂x = 0 From dv dt = v, v ∂ ∂x = ∂ ∂t is obtained, so:

∂Ey

∂x − ∂Ex

∂y = v c 2

∂Ey

∂t

Combine these two formulas with the above three components of dB⃗ dt = V⃗ × dE⃗ dtc 2 :

∂Bx

∂t = 0

∂By

∂t = v c 2

∂Ez

∂t ∂Bz

∂t = − v c 2

∂Ey

∂t

By comparison, we can get:

∂Ez

∂y − ∂Ey

∂z = 0

∂Ex

∂z − ∂Ez

∂x = − ∂By

∂t ∂Ey

∂x − ∂Ex

∂y = − ∂Bz

∂t

Combining the above three formulas, it is Faraday’s electromagnetic induction equation:

∇ × E⃗ = − ∂B⃗ ∂t

5Next, we analyze the gravitational field A⃗ equation dB⃗ dt = dV⃗ dt × E⃗ c 2 caused by the change of magnetic field B⃗ . The three components of the equation are as follows:

∂Bx

∂t = 0

∂By

∂t = ∂V⃗ ∂t × Ez

c 2 = A⃗ × Ez

c 2

∂Bz

∂t = − ∂V⃗ ∂t × Ey

c 2 = −A⃗ × Ey

c 2

The differential sign d has been changed to a partial differential sign ∂. Where the direction of A⃗ is the acceleration direction of space point P, which is opposite to the positive direction of X axis. The above equation can be written as dB⃗ dt = A⃗× E⃗ c 2 , which can be understood as: When the positive charge point O accelerates along the positive direction of the X axis, at any point P in the surrounding space, a changing magnetic field

dB⃗ dt , an electric field E⃗ and a gravitational field A⃗ opposite to the acceleration direction are generated. A⃗, E⃗ and dB⃗ dt are perpendicular to each other, satisfying the cross-multiplication relation, and constructing a cylindrical spiral. In the unified field theory, the essence of the field is the space that moves in a cylindrical spiral. From the equation dB⃗ dt = dV⃗ dt × E⃗ c 2 +V⃗ × dE⃗ dtc2 : V⃗ × dE⃗ dtc2 represents the eddy electric field generated by the change of magnetic field, which is the Faraday electromagnetic induction principle. dB⃗ dt = dV⃗ dt × E⃗ c 2 is the vortex gravitational field generated by the change of magnetic field. Since the change of magnetic field produces eddy electric field, it satisfies the left-handed spiral. The vortex gravitational field generated by the changing magnetic field should also be a left-handed spiral, because dV⃗ dt × E⃗ c 2 and V⃗ × dE⃗ dtc2 are both positive signs. Now, after a lot of experiments, this point has also been confirmed. 6